Lunes 6 de Abril
En esta clase la Ing. Mónica Mantilla se presento e indico que impartiría la materia de calculo vectorial, para lo cual nos dio varias indicaciones en las cuales estaba crearnos un blog con una cuenta de Gmail ya partir de eso debemos subirlo a la pagina donde la Ingeniera nos revisara todo lo que es necesario como nuestro perfil, pestañas con los meses y evidencias en las cuales debemos ir resumiendo cada clase que imparta y en las evidencias escanear cada tarea que nos haya revisado esto será revisado el lunes 13 de Abril.
SEMANA 2
Jueves 16 de Abril
En esta clase la Ingeniera Mantilla impartió la primera clase y el tema fué acerca de LA GEOMETRÍA EN EL ESPACIO, empezamos con funciones implícitas de dos variables y que geométrica mente en R2 representa una curva, con sus respectivos ejemplos. A continuación vimos las funciones implícitas en R3 las cuales geométrica mente representan una superficie, con un caso particular el cuál indica que una función implícita que representa en R3 una superficie con generatriz paralela al eje Oz, si esta en el plano es una curva y si esta en el espacio es una superficie. La recta en el espacio con la respectiva ecuación vectorial de la recta, las ecuaciones simétricas, canónicas o cartesianas de la recta. La recta es un caso particular de una curva ALABEADA. con la respectiva ecuación vectorial de la recta dado dos puntos.
SEMANA 3
lunes 20 de abril
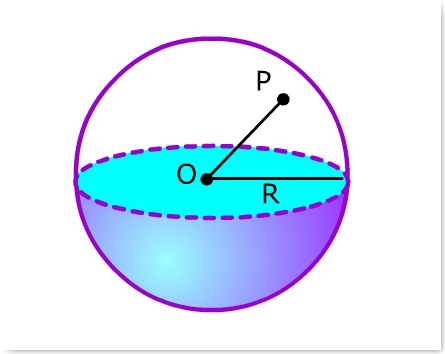
Ecuación General de una esfera
Datos: O(x0, y0, z0) y Radio R

Un caso particular de esta es cuando en centro esta en el origen de coordenadas.

Superficies en R3: Para determinar en una función que tipo de superficie tiene en el espacio se necesitó un Analisis. Al final de este proceso, si se lo realizo correctamente, el resultado era la grafica de la superficie en R3.
Análisis de las Superficies en R3
Semana 4
Se Estudió un nuevo tema Funciones Vectoriales
Funciones Vectoriales: Las funciones vectoriales pueden tener "n" componentes:
Se analizaron ciertos conceptos que se aplican tambien a estas Funciones
Dominio
Si r(t) = ( f1(t), f2(t), f3(t) )
DomF es la interseccion de los dominios de cada función (Df1, Df2 y Df3 )
Límites y Continuidad: Se evalua cada limite y si los limites exiten y son iguales a L estos también son continuos.
Derivadas: Si la función es continua en un intervalo y tiene un dominio definido entonces:
Se observo algunas aplicaciones:
Semana 5 (28 al 29 oct.)
Se calcula el vector Tangente del triedro, debido a que de este dependen todos los cálculos posteriores. Para calcularlo se utiliza la siguiente fórmula:
*Donde r (t) es el vector que define a nuestra curva parametrizada, r’(t) es su derivada y
Como segundo paso se calcula el vector Binormal del triedro, usando la fórmula:
+ r´´(t)
N = B x T
Ecuaciones de Frenet - Serret


SEMANA 3
lunes 20 de abril
Ecuación General de una esfera
Datos: O(x0, y0, z0) y Radio R

Un caso particular de esta es cuando en centro esta en el origen de coordenadas.

Se terminó un ejercicio de aplicación de la Ecuación de la Esfera y se continuo con el tema nuevo Superficies en R3
Superficies en R3: Para determinar en una función que tipo de superficie tiene en el espacio se necesitó un Analisis. Al final de este proceso, si se lo realizo correctamente, el resultado era la grafica de la superficie en R3.
Análisis de las Superficies en R3
Se enunciaban tres pasos, para ubicar a la superficie en el espacio tridimensional:
1. Intersección con los ejes coordenados: OX, OY y OZ.
2. Intersección con los planos coordenados: XOY, YOZ y XOZ
3. Intersección con los planos paralelos a los coordenados XOY, YOZ y XOZ.
Consideraciones:
- En el paso 1, la intersección con los ejes daba como resultado puntos. Si en cualquiera de los ejes se encontraba con una igualdad no existente se consideraba que la superficie con interseca con este eje.
- En el paso 2 y 3, la intersección con los planos daba como resulta curvas. En el paso 2, dependiendo de que función se analizaba podía ocurrir que no intersecaba con algun plano coordenado.
- Al final se tomaba todas la trazas, es decir los graficos de cada proceso; se los juntaba y el resultado final era la Superficie de la función.
JUEVES 23 DE ABRIL
Se realizaron aplicaciones del Análisis de Superficies. Aquí algunos ejemplos revisados tanto en clases como en el libro de Stewart.
27 DE ABRIL
PRUEBA 1
Se Estudió un nuevo tema Funciones Vectoriales
Funciones Vectoriales: Las funciones vectoriales pueden tener "n" componentes:
F(t) = (f1(t), f2(t), ....... fn(t))
Para nuestro curso se trabaja hasta 3 componentes por que se trabaja en R3 es decir un espacio de tres dimensiones. Las Funciones vectoriales se representan:
r(t) = ( f(t), g(t), h(t) )
Se analizaron ciertos conceptos que se aplican tambien a estas Funciones
Dominio
Si r(t) = ( f1(t), f2(t), f3(t) )
DomF es la interseccion de los dominios de cada función (Df1, Df2 y Df3 )
Límites y Continuidad: Se evalua cada limite y si los limites exiten y son iguales a L estos también son continuos.
r'(t) = ( f1'(t), f2'(t), f3'(t) )
Integrales: Sabiendo que p,q,r representan a f1, f2 y f3
Se observo algunas aplicaciones:
Helice Circular
Nudo de Trébol
Espiral Toroidal
Martes 28 Oct: Se aplicó un taller de Integrales y Derivadas de Funciones Vectoriales entregado al finalizar la Clase y se empezoó el tema Triedro Móvil
Tiedro Móvil: En el Triedro Movil se destaca las rectas y los planos que son participes de su movimiento.
Rectas: Tangecial (T), Recta Binormal (B) y Recta Normal Principal (N).
Planos: Osculador (T y N), Rectificante (T y B), Normal Principal (N y B).
En esta clase se dedujó las Fórmulas de los Vectores Tangencial, Binormal y Normal Principal.
Vector Tangente.
*Donde r (t) es el vector que define a nuestra curva parametrizada, r’(t) es su derivada y
Vector Binormal .
Vector Normal Principal.
Finalmente para completar el Triedro de Frenet, se determina el vector Normal Principal, el cual es normal al Vector Tangente y al Vector Binormal, de ahí que podamos calcularlo mediante un simple producto vectorial entre ambos vectores:
N = B x T
Miércoles 29 Oct: Para finalizar el primer mes de clases se estudio las Ecuaciones de Frenet - Serret. Se las Obtuvo partinedo del concepto de longitud de arco. Además, se analizó las Clases de Curvaturas
Ecuaciones de Frenet - Serret
Donde (K) es la curvatura de Flexión y (T) es la curvatura de Torsión.
Clases de Curvatura
Curvatura de Flexión (K): Se define como la razón instantánea de cambio de dirección de los puntos de la curva C, con respecto a la longitud de arco.
Curvatura de Torsión (T): Esta nos indica el alejamiento y acercamiento de la curva al plano osculador.
.gif)

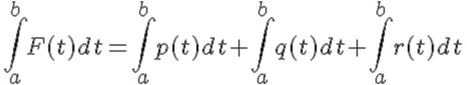






Este comentario ha sido eliminado por el autor.
ResponderEliminar